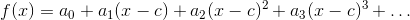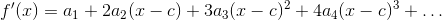(#1) The dark side of the most beautiful equation

'i' be real or 'π' be rational

Jan 16, 2021

(reading time: 10-22 mins - depending on how long you spend on mathematics below)

Euler’s equation

is undoubtedly the most beautiful equation in the entire mathematics that comprises the five most important mathematical constants.

The numbers 0 and 1
e, an irrational number (with unending digits). It is the base of natural logarithms that arises naturally through study of compound interest
π, also an irrational number
i, defined as the square root of negative one: √(-1)

But this beautiful equation has a history and a dark past. A past which is far more intriguing than any Sherlock Holmes mystery. The past which

spans over a millennia starting from few hundred years BC and culminating after WW II,
is build on the contributions from some of the oldest civilizations in China, India and Persia before receiving finishing touches during Renaissance period in Europe,
consists of deception, rivalry, adultery, murders and beheading
is sculpted by Archimedes, Euler, Madhava of Sangramma, Pythogoras, Scipione del Ferro, Gerolamo Cardano

I’m going to unravel the story and explore the dark sides of the mathematical belly of the history.

The story has few sub-plots all moving more or less parallel to each other oblivious to the existence of other.

I’m gonna call these plots, e, π, i and 1/0 and explore them all before putting them together.

1. e

Ok, lets start from the Swiss Alps in the year 1655, birth year of Jacob Bernoulli.
He had great interest in Mathematics. Somewhere in late 1670s on the insistence of his father he chose a better paying profession - business over mathematics. While Newton in neighboring country was churning out laws of motion, Bernoulli was pondering over the problem of compounding interest described below:
- A bank account starts with $1 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2. What happens if the interest is computed and credited more frequently during the year?
- lets try to break it down:
- If the interest is credited twice in the year, the interest rate for each 6 months will be 50%, so the initial $1 is multiplied by 1.5 twice, yielding $1 × 1.52 = $2.25 at the end of the year.
- compounding quarterly yields $1 × 1.254 = $2.4414..., and
- compounding monthly yields $1 × (1 + 1/12)12 = $2.613035…
- If there are n compounding intervals, the interest for each interval will be 100%/n and the value at the end of the year will be $1 × (1 + 1/n)^n.
- we are down to calculating limit. As n approaches infinity what does (1+1/n)^n approaches to.
- This can be easily proved using special case of Taylor series (called Binomial Series) to be equal to 2.71828
- and this is how our little friend ‘e’ saw the light of the day in 17th century.
In case you are wondering, e is the natural rate of growth. Notice the rate of growth coming almost to a halt in above example. Well, this is how the nature allows growth - look at plants, trees, humans - all grow at de-accelerating rate before almost coming to a halt as adulthood approaches but the actual growth never stops - it just tends to a maximum limit.

2. π

No story in mathematics is as interesting as of π. The circular shape has mesmerized, revolutionized and as well as baffled humans since the dawn of the early civilizations.

Archimedes in 220 BC took up the challenge of finding the value of π; in fact this was the last problem that he focussed before he was killed by Roman soldiers (trivia: Archimedes’ last words before being killed by Roman soldiers were ‘don’t disturb my circles’).
“don’t disturb my circles”, cried Archimedes
Archimedes used the method of exhaustion (as was used by Chinese folks few centuries earlier). Method of exhaustion is nothing but progressively constructing regular polygons with more and more sides to reach the shape of circle and finding the circumference by measuring the sides of such polygon.
Study of π died with Archimedes for at least a 1000 years before it was solved more precisely by an Indian mathematician Madhava of Sangamagrama in 14th century.
Madhava calculated value of π using below mentioned infinite series notation:
$\theta =\tan \theta -{\frac {\tan ^{3}\theta }{3}}+{\frac {\tan ^{5}\theta }{5}}-{\frac {\tan ^{7}\theta }{7}}+\cdots$
value of π is obtained by substituting arctan(1) (read as tan inverse of 1 - which is equal to π/4) for 𝜃 in above equation.
Madhava’s trignometric infinite series were re-discovered by Europeans most notably by - James Gregory, Leibniz and others few centuries later.

3. i

Well this is a tricky customer to explain. The 16th-century Italian mathematician Gerolamo Cardano is credited with introducing complex numbers—in his attempts to find solutions to cubic equations.
I have chronicled the detailed story of Cardano, a brilliant mathematician, a gambler and a Doctor by profession in this letter.
Give it a read, and come back to continue from below.
So we now know the back story of i, π and e. But what led to their marriage and the origins of one of the finest equations known to man… errr…..I mean human.

4. Taylor Series

The Taylor expansion is one of the most beautiful ideas in mathematics.

The idea is thus: for every continuous function, we should be able to write down a polynomial that approximates it. And in fact, if our polynomial contains enough number of terms it will exactly equal the original function.

The idea behind the Taylor expansion is that we can re-write every smooth function as an infinite sum of polynomial terms. The first step is therefore to write down a general nth-degree polynomial. Here it is:

The goal here is to find a clever way to find the coefficients a0, a1, … in that equation, given some function f and an initial value of c. Here is the logic for doing that. Polynomials are smooth, so that guarantees they’re differentiable. That is, we can calculate the first, second, third and so on derivatives of them.

So starting with our polynomial above, let’s take the first few derivatives of it, like this:

Now that we have n derivatives of f, let’s evaluate them for some number that will cause most of their terms to drop away. This is the key step. If we’re clever, we’ll notice that if we evaluate them at x = c, most of their terms will go to zero.

Our original equation now becomes:

This equation is what we’re looking for. It gives a polynomial expansion for every smooth function f.

When c=0, the formula slightly changes. This new formula below is called Maclaurin series:

f(x) = f(0) + x¹ f’(0) / 1! + x² f’’(0) / 2! + x³ f’’’(0) / 3! + x⁴ f’’’’(0) / 4! + …

Now lets calculate

f(x) = sin(x)
sin(x) = 0 + x¹*1/1 - x²*0/2 - x³*1/6 + x⁴*0/24 + …
sin(x) = 0 + x¹/1 - x³/6 + …
f(x) = cos(x)
cos(x) = cos(0) — x¹sin(0)/1! — x²cos(0)/2! + x³sin(0)/3! + x⁴cos(0)/4! + …
cos(x) = 1 - x²/2 + x⁴/24 - …
f(x) = e^(x)
e^(x) = 1 + x¹/1 + x²/2 + x³/6 + x⁴/24 + …
e^(ix) = 1 + i¹x¹/1 + i²x²/2 + i³x³/6 + i⁴x⁴/24 + …
e^(ix) = 1 + ix/1 - x²/2! + i³x³/6 + x⁴/24 + …
e^(ix) = (1- x²/2! + x⁴/24 + …) + (ix/1 + i³x³/6 + …)

resulting in

e^(ix) = cos(x) + i*sin(x)

5. Euler Identity

substituting x = π in equation above

gives us

e^iπ + 1 = 0

essentially,

adding 1 to an irrational number (e) raised to the power of another not only irrational but unreal number (iπ) gives you nothing (0)

Science, Tech and History

Discussion about this post